Któż z nas nie chciałby uchylić zasłony, za którą kryje się przyszłość; rzucić okiem na postępy nauki i tajemnice jej rozwoju w nadchodzących stuleciach? Historia daje nam lekcję ciągłości rozwoju nauki. Wiemy, że każda epoka ma swoje własne problemy, które następna rozwiązuje albo porzuca jako nieistotne, a jednocześnie tworzy nowe. Jeżeli chcemy uzyskać wgląd w możliwy rozwój wiedzy matematycznej w najbliższej przyszłości, to musimy przyjrzeć się nierozwiązanym kwestiom i rozważyć pytania stawiane przez dzisiejszą naukę, a których rozwiązania oczekujemy w przyszłości.
David Hilbert, The 23 Problems (1900)

Warianty fasady budynku Muzeum Sztuki w Bejrucie, (c) HW Architecture
Nie da się mówić o przygodności i ryzyku bez odwoływania się do pojęcia przypadku. Gdy rzeczy wydarzają się przypadkowo, oznacza to, że nie stosują się w tym względzie do żadnego określonego prawa. Przypadek oswoiło dopiero odkrycie prawidłowości statystycznych1. Naukowcy i metafizycy zaczęli mówić o regułach rządzących zdarzeniami losowymi i badać prawdopodobieństwo. Tak narodziła się probabilistyka2. Odkryto, że u swej podstawy nawet prawa fizyki są niedeterministyczne3.
Losowość związana jest ze statystyką i prawdopodobieństwem. Wyobrażamy sobie procesy losowe, a więc powtórzenia eksperymentu losowego. Mówiąc o powtórzeniu, zakładamy istnienie określonego układu, w ramach którego eksperyment ma miejsce i może być wielokrotnie powtarzany. Za przypadkiem kryje się zatem to, co stałe. Wyniki są różne, ale układ wyjściowy ten sam. Trudno mówić o losowości, jeśli jakiś przypadkowy fakt wystąpił jednorazowo. Lepiej jest wtedy użyć określenia zdarzenie.
Filozofia zdarzenia różni się od filozofii prawdopodobieństwa. Przyszłość jest prawdziwie nieznana. Nie istnieje skończona lista możliwych scenariuszy. Nawet jeżeli wszystkie przyszłe rozwiązania, jakie świat kiedykolwiek wylosuje, znajdują się w „przestrzeni probabilistycznej” – jak wymaga tego aksjomatyczna teoria prawdopodobieństwa – to scenariusze, czyli opisy tego, co może się wydarzyć, tak jak i same potencjalne zdarzenia, nie są uprzednio dane. Stają się możliwe do pomyślenia i opowiedzenia dopiero po niemierzalnym wystąpieniu. „Algebra zdarzeń” zostaje tu głęboko przekalibrowana.
Pozostaje zatem kwestią czysto metafizycznej decyzji, czy uznamy, że zdarzenia losowały się z większego zbioru, czy też raczej wynurzyły z próżni, a żadnej urny z losami nie było. Nie ma to znaczenia dla fizycznych obiektów, których los jest przypisany do miejsca i nie może być nie z tego świata. Dla nich stworzono teorię prawdopodobieństwa, by z czasem dojść do łańcuchów Markowa, gdzie stan obiektu rozpoznawany jest jako zasadnicza zmienna i przez ekstrapolację może być mylony ze stanem świata. Jest to jedynie metafora, mająca pasować do wielkości fizycznego obiektu i nie powinno się jej ekstrapolować na cały świat.
Teorii prawdopodobieństwa nie stworzono z myślą o bytach metafizycznych, takich jak świat czy rynek. W odniesieniu do nich lepiej jest mówić nie o możliwości, lecz o kontyngencji. Powiedzieć, że dana rzecz jest kontyngentna, znaczy tyle, że może być ona inna niż jest, bez określania jej stanu, albo powiedzieć, jakimi innymi rzeczami mogłaby być. Mogłaby być zupełnie inna. W gruncie rzeczy mogłaby być inna od tego, czym jest, w sensie nie bycia w ogóle – warunek nie do utrzymania dla pojęcia stanu możliwego.
1. Wszechświat i świat
To fascynujące, że Hilbert mówi o odkrywaniu przyszłości w odniesieniu do matematyki. Mówi o „ciągłości” historii i oddaje się spekulacjom. Próbuje konstruktywnie przewidzieć przyszłość matematyki, identyfikując jej obecne problemy i oferując wskazówki co do ich przyszłego rozwiązania. Ciekawie jest zdać sobie sprawę, że historia tych problemów potoczyła się zupełnie inaczej, w sposób nieciągły, by ująć rzecz oględnie, i nie do pomyślenia dla samego Hilberta. Twierdzenie o niezupełności, udowodnione przez austriackiego matematyka Kurta Gödla w 1931 roku, wywróciło program Hilberta do góry nogami. Hilbert mówił o „możliwym rozwoju” matematyki, podczas gdy bardziej stosowne byłoby określenie „zdarzenie” albo „zmiana paradygmatu”. W istocie szósty problem na liście Hilberta dotyczył ufundowania prawdopodobieństwa na teorii aksjomatycznej.
Hilbert przedstawił swoją listę 23 zagadnień na inauguracji Międzynarodowego Kongresu Matematyków w Paryżu w roku 1900. Tłem była wystawa światowa i najnowsza atrakcja francuskiej stolicy – wieża Eiffla, wzniesiona na otwarcie poprzedniej wystawy w 1889 r. Powiedzieć, że Hilbert spekulował, próbując odsłonić przyszłość matematyki za pomocą swojej listy 23 problemów, to powiedzieć za mało. Hilbert spekulował podwójnie. W istocie drugi problem na liście stanowił pierwszy krok na drodze do rozwiązania wszelkich przyszłych problemów w matematyce: skonstruować uniwersalny algorytm, oceniający prawdę lub fałsz twierdzenia matematycznego. Spekulacja Hilberta była więc gorzej niż uniwersalna: była końcem świata matematyki; jej celem było unieszkodliwienie każdego matematycznego problemu.
Teoria prawdopodobieństwa mówi o wszechświecie lub przestrzeni probabilistycznej. Markus Gabriel dokonuje rozróżnienia pomiędzy wszechświatem a światem4. Wszechświat jest zbiorem fizycznych obiektów, opisanym przez prawa, do których się one stosują. Świat jest pojęciem o wiele szerszym. Istnieje świat fizyczny, ale także świat snów, świat sztuki, świat kochanków, świat książek i tak dalej – jak również świat człowieka. Zwykle mówimy raczej o końcu świata niż wszechświata, a Heidegger ukuje określenie „bycie-w-świecie”. Gabriel przekonuje nawet, że świat nie może istnieć, ponieważ nie może istnieć całość rzeczy wyobrażalnych. Użycie słowa „świat” wskazuje zwykle na dyskurs raczej metafizyczny niż fizyczny.
Zauważmy, że wystawy w 1889 i 1900 roku, poprzedzające odpowiednio wzniesienie wieży Eiffla i prezentację 23 problemów przez Hilberta, nosiły miano „uniwersalnych” [Exposition Universelle], a Luwr uważany jest za „uniwersalne” muzeum. Zanim postanowiono, że to Luwr użyczy nazwy i dostarczy treści, architektowi w Abu Zabi zlecono zaprojektowanie „muzeum uniwersalnego”. Muzeum jest uniwersalne, gdy jest transhistoryczne i transgeograficzne; gromadzi i udostępnia artefakty stworzone przez człowieka we wszystkich zamieszkałych miejscach świata, przez całe dzieje ludzkości. Jest więc krańcem wszystkich kolekcji, rodzajem końca świata.
Gdy podpisano porozumienie rządu Francji z Emiratem Abu Zabi i ogłoszono, że paryski Luwr użyczy swej marki nowemu muzeum, wielu było zaskoczonych, a nawet zgorszonych. Oto nazwa „Luwr” miała się pojawić pośród pustyni; ukuto nawet określenie „pustynny Luwr”. Do końca świata, kresu wszystkich epok i wszystkich kolekcji, dodaliśmy właśnie kolejne trzęsienie ziemi. Luwr był teraz podwójnie uniwersalny – nie tylko stawiał sobie za cel objęcie wszystkich miejsc i wszystkich czasów, lecz sam nie był już przywiązany do żadnego konkretnego miejsca ani czasu. Mógł się mieścić zarówno w Paryżu, jak i w Abu Zabi, zarówno w naszej przyszłości, jak i przeszłości. Stał się muzeum uniwersalnie uniwersalnym, rozwijającym się i trwającym wiecznie. W pewnym sensie była to również próba rozwiązania wszystkich przyszłych problemów. Prawdziwe wyzwanie dla architekta, ale i znów spekulacja.

Louvre Abu-Dhabi, © TDIC, Architekt: Ateliers Jean Nouvel.

Louvre Abu-Dhabi, © TDIC, Architekt: Ateliers Jean Nouvel
2. Spekulacja
W 1900 roku Bachelier opublikował swoją Teorię spekulacji. Opisał w niej mechanikę giełdy, a zwłaszcza transakcje „z premią”, znane dzisiaj jako opcje, a bardziej ogólnie jako instrumenty pochodne. W efekcie podał nawet pierwsze (heurystyczne) matematyczne ujęcie ruchów Browna. Bachelierowski wzór na cenę opcji jest niemal identyczny z tym, który w 1973 roku wyprowadzą Fischer Black i Myron Scholes.
Szósty problem Hilberta został przedstawiony w 1900 r. i rozwiązany w 1933 r., gdy Kołmogorow opublikował swoją monografię i stworzył aksjomatyczną podstawę teorii prawdopodobieństwa. Spekulacja Bacheliera była również spekulacją w tym sensie, że ruch Browna – którego nie określał tym mianem – nie został jeszcze matematycznie udowodniony. Dokonał tego Wiener dopiero w 1920 r., korzystając z osiągnięć, jakie poczynił w analizie procesów stochastycznych Percy John Daniell, prekursor Kołmogorowa. We współczesnych podręcznikach ruch Browna (proces Wienera) opisuje się zwykle za pomocą twierdzenia Kołmogorowa o ciągłości procesów, to znaczy aksjomatycznej teorii przezeń wyłożonej.
Rynek przeżył krach w 1929 r. i handel opcjami został zakazany, gdyż kupowanie opisanych przez Bacheliera opcji put uznano za obstawianie przeciwko dobru kraju. Opcje put wróciły do łask w 1973 r., gdy Black i Scholes podali dokładny wzór wyceny optymalnej ceny opcji. Opcja (kupna lub sprzedaży), czy ogólniej derywatyw (instrument pochodny), nie były już postrzegane jako spekulacja na danym aktywie, lecz przedłużenie jego samego i obrotu nim. Black, Scholes i Merton udowodnili, że derywaty są w istocie redundantne względem danego waloru. Odtąd opcje można było tworzyć bezpiecznie; handel nimi nie był już spekulacją, ale przemysłem, a na parkietach giełdowych po 1973 roku pojawiły się tłumy maklerów opcji.
Kolejny krach nastąpił w 1987 r. właśnie dlatego, że traderzy – polegając na algorytmie Blacka-Scholesa-Mertona (BSM) – zostawili komputerom syntetyzację i handel opcjami, podczas gdy opcje wcale nie były redundantne. W gruncie rzeczy krach z października 1987 r. oznaczał prawdziwe narodziny rynku opcji, w tym sensie, że narzucił niezależny handel nimi (tzw. uśmiech zmienności). W ostatecznym rozrachunku opcje nie są ani hazardem, ani strukturami redundantnymi. Oba te probabilistyczne ujęcia są błędne. Opcje nie są uzupełnieniem, naddatkiem, pasożytem, nie są niebezpieczne ani szkodliwe. Są niezależnymi walorami. Być niezależnym, to nie to samo, co być niebezpiecznym. By podkreślić niezależność derywatów i ich zalety, wolę nazywać je „kontyngentnymi roszczeniami” [contingent claims].
3. Bejrut
W 1929 r. Charles Corm zbudował według własnego projektu swój słynny drapacz chmur, który przez jakiś czas był najwyższym budynkiem w Bejrucie. Inspirowany nowojorskim Chrysler Building, budynek Corma był siedzibą firmy, którą ten założył po ubiciu targu z Henrym Fordem (z którym spotkał się był we wczesnych latach 20. XX wieku w Nowym Jorku) – przedstawicielstwa Ford Motor Company na Bliski Wschód. Budynek znany był pierwotnie jako The Ford Motor Company’s Middle East Headquarters, później przemianowano go na The Corm Building and Gardens. Idea była taka, żeby montować Forda Model T na miejscu i rozwijać sieć dystrybucji na cały region.
Ford Model T narodził się w 1908 r., na rok przed tym, jak Émile Borel nieoczekiwanie udowodnił twierdzenie, znane jako mocne prawo wielkich liczb. Powiada się, że sukces rynkowy auta, sprzedawanego na całym Bliskim Wschodzie przez liczne oddziały firmy Corma, przyczynił się do powstania sieci dróg w regionie, a pośrednio do narodzin państw naftowych. Działka Corma w Bejrucie znajdowała się na samym początku Drogi Damasceńskiej, budynek wzniósł jednak nieco z tyłu, by w razie trzęsienia ziemi nie zawalił się i nie zatarasował tej tak ważnej dla Bliskiego Wschodu trasy.
Przez jakiś czas wieża Eiffla była najwyższym budynkiem na świecie; potem zdetronizował ją nowojorski Chrysler Building. W starożytności w Bejrucie rozwinęła się jedna z wiodących szkół prawa rzymskiego. Prawo i sądy są pierwotną siedzibą prawdopodobieństwa: gdy mówi się o „udowodnieniu” winy oskarżonego, ma się na myśli „uprawdopodobnienie”. W nowoczesnej historii teorii prawdopodobieństwa rozróżniamy szkołę francuską (Borel, Lebesque, Fréchet, Lévy) i rosyjską (Markow, Kołmogorow, Czebyszow). Mówi się, że przez 5000 lat swego istnienia Bejrut był burzony i odbudowywany siedem razy.
Nassim Taleb, makler opcji w burzliwych dniach krachu 1987 roku, autor Czarnego łabędzia i jeden z pierwszych krytyków prawdopodobieństwa w odniesieniu do rynku instrumentów pochodnych, urodził się w Amioun, niecałe 80 kilometrów od Bejrutu. Wiodąca dzisiaj firma produkująca oprogramowanie do handlu opcjami (pierwsza, która nadała każdej opcji odrębny tzw. numer zmienności, zgodnie z logiką „uśmiechu zmienności” i wbrew całemu paradygmatowi modelu BSM) powstała po krachu giełdowym 1987 roku, założona przez dwóch braci urodzonych w Bejrucie.
Starszy z braci, inżynier i pasjonat chemii, został jednym z największych na świecie zbieraczy minerałów i kryształów. W 2013 r. przekazał swoją kolekcję do muzeum, które zbudował w Bejrucie, naprzeciwko ogrodów budynku Corma i jeszcze bliżej Drogi Damasceńskiej.
Młodszy z braci był moim szefem, gdy zaczynałem karierę jako trader opcji. Los sprawił, że pierwszym dniem mojej pracy był dzień krachu, 19 października 1987 r. Ja też urodziłem się w Bejrucie, a dwie książki, które napisałem, by wyjaśnić zjawisko „uśmiechu zmienności” i to, jak przeczy ono modelowi Blacka-Scholesa, noszą podtytuły odpowiednio The End of Probability [Koniec prawdopodobieństwa] i An Inverse View of the Market [Odwrotne spojrzenie na rynek]5.
4. Prawdopodobieństwo
By sformalizować teorię prawdopodobieństwa i rozwiązać szósty problem Hilberta, Kołmogorow wprowadził pojęcie przestrzeni zdarzeń elementarnych [sample space]. Jest to wielka urna, określana również jako wszechświat (Ω), z której świat losuje konkretne rozwiązania czy przypadki (ω). Zdarzenie elementarne, czyli to, co się konkretnie wydarza, kontyngentne „to” (jak w wyrażeniu „to się stało”), jest niemierzalne i nieopisywalne. Może być nawet niewyobrażalne, to znaczy możliwe do wyobrażenia tylko przez Boga. Zdarzenia elementarne są z definicji powiązane ze światem konkretnym; świat konkretny może istnieć wyłącznie jako część obrazu losowości; a zatem u podstaw każdego zdarzenia leży – a nawet owo zdarzenie wywołuje – pojęcie konkretnej próbki.
Gdy rzucamy kostką, interesują nas tylko zdarzenia opisane liczbą wyrzuconych oczek, ponieważ przyjmujemy perspektywę gry w kości. Gra czy też rzeczywistość, którą wtedy rozważamy, jest ekranem, abstrakcją świata konkretnego. Oddzielamy konkretne od abstrakcyjnego i rozróżniamy pomiędzy absolutnie konkretną sytuacją a dającą się pomyśleć rzeczywistością. W istocie to, czym jest próbka w swej absolutnej konkretności, albo co świat w gruncie rzeczy uzyskał, by rzut mógł się odbyć, nie kończy się na liczbie oczek na wierzchniej ściance kostki, lecz rozciąga się w niewyobrażalną otchłań całej konkretnej sytuacji.
Użyłem słowa „całej”. Oznacza to, że opisanie całej sytuacji wymaga postawienia pytania, czy w chwili rzutu było słonecznie czy pochmurno, czy rzucający uśmiechał się czy krzywił, czy miał dość siły w ręce, by podnieść kostkę i wykonać rzucić, czy przyciąganie ziemskie było na tyle stałe, żeby zbliżyć kostkę do podłoża i tak dalej.
Chociaż niewątpliwie otchłanny, świat konkretny – tak jak przedstawia go formalizm teorii prawdopodobieństwa – jest niekompatybilny z radykalnym zdarzeniem. Opis sytuacji w jej absolutnej konkretności praktycznie nie ma końca, możemy bowiem w nieskończoność uszczegóławiać wyjściowe zdarzenie „wypadło sześć”, mówiąc, że kostka była czerwona, gracz się uśmiechał, słońce świeciło, a grawitacja działała, do czego moglibyśmy następnie dodać, że przy drugim rzucie wypadło cztery, a przy trzecim dwa, albo że przy setnym rzucie padał deszcz, a przy milionowym spadający meteoryt zabił rzucającego i tak dalej, bo wszystko, co wydarzyło się dotychczas w historii wszechświata może być uważane za pojedynczą próbkę, którą świat wylosował, raz i na zawsze, od początku aż po kres czasu. Na jakimś poziomie otchłani powstaje cięcie, wyróżniony zostaje punkt widzenia, ze świata wykrojony zostaje fizyczny obiekt (kostka), a to automatycznie oznacza, że obiekt ma wiele ścian, a wielokrotne próby mogą dawać ten sam wynik, różniąc się tym tylko, czego w danej perspektywie nie sposób już dostrzec. To powoduje powtórzenie, a zatem losowość w zwykłym znaczeniu tego słowa. Zawiesiwszy upadek i przełamawszy „raz i na zawsze”, możemy tylko powtarzać.
W istocie nie powinniśmy nigdy cofać się myślą ku wszechogarniającej przestrzeni zdarzeń. Teorii prawdopodobieństwa nie powinno się ekstrapolować poza jej skromny model. Miała ona jedynie dotyczyć zsumowanego raz na zawsze wszechświata rzeczy, a nie świata. Być może jednak należy poszukiwać nowej metafizyki przypadku poza teorią prawdopodobieństwa i kwestionować całą logikę abstrakcji. Co byłoby alternatywą? Logika, w świetle której otchłań nie jest już bierną i wsteczną przyczyną losowości, lecz jest spontanicznie rzutowana naprzód.
5. Giełda
Pieniądz zostaje wynaleziony i staje się jedynym kresem świata. Pieniądze można tylko zarabiać albo tracić. Cena akcji może tylko wzrosnąć albo spaść. Gdy dana jest giełda, dana jest losowość. Infrastruktura przestrzeni zdarzeń nie jest już potrzebna. Spekulacja – autorefleksja rynku – staje się jedynym, nieustająco zmiennym gruntem.
Teoria prawdopodobieństwa należy do domeny abstrakcji, podczas gdy pieniądze i cena są konkretem. Zdarzenia teorii prawdopodobieństwa (to znaczy dającej się pomyśleć rzeczywistości) nawiązały kontakt z absolutnym konkretem jedynie wstecznie. Jak powiedzieliśmy, pod powierzchnią rzeczy drążona była otchłań, w desperackiej próbie zrekonstruowania przyszłości jako obecnej w teraźniejszości, jako istniejącego elementu całości. Jednak przyszłość nie powinna być częścią absolutnego konkretu, a na pewno nie przy logice, w ramach której wszelka różnica jest przepisywana w przeszłości! Nie powinna być uszczegółowieniem tego, co los, raz i na zawsze, trzyma dla nas w zanadrzu! Przyszłość powinna być absolutnie inna, absolutnie kontyngentna. Powinna być inna, ale nie wiemy od czego.
W jaki sposób otchłań mogłaby być rzutowana naprzód? Jak konkretny świat, teraz przesłonięty przez pieniądze, mógłby odzyskać swe absolutne bogactwo i nieskończoność detalu? Jak przyszłość mogłaby być konkretna, a jednocześnie absolutnie otwarta? Odpowiedzią jest rynek kontyngentnych roszczeń, ostateczna konsekwencja istnienia pieniędzy i handlu.
Handlu nie da się sprowadzić do wyciągania losu z urny. Handel znaczy losowość. A zatem gdy stochastyczne procesy, które piszemy w świecie finansów, zwłaszcza ruch Browna, nie są już postrzegane jako wynik abstrakcji otchłannego konkretu, lecz konceptualizacji giełdowego parkietu, gdy nie ma już przestrzeni zdarzeń, z której ciągnie się losy, lecz tylko cena o jedynym możliwym losie (rosnąca albo spadająca) i pieniądze o jedynym możliwym losie (zarabiane lub tracone), Black, Scholes i Merton pokazują, że ta nowa wizja losowości, intensywna, a nie ekstensywna, już nie jako sekwencja losowań, lecz jako zintegrowana strategia handlowa, jest odpowiednikiem replikacji kontyngentnych rozliczeń, a zatem pisania kontyngentnych roszczeń. Te ostatnie, gdy zostaną już napisane, mogą być tylko przehandlowane, gdyż przestrzeń zdarzeń skurczyła się, a jedynym wolnym miejscem jest giełdowy parkiet.
Handel daną akcją jest tym samym, co stworzenie opcji na nią, jest tym samym co handel tą opcją, jest tym samym co stworzenie opcji na opcję, jest tym samym co handel opcją na opcję, i tak dalej. Nieskończoność konkretnego świata zostaje jednym ruchem odwrócona, by już nigdy nie zsumować się we wszechświecie przypadków. Otchłań otwiera się spontanicznie naprzód. Kołmogorow umiera 20 października 1987 roku.
6. Pustynia
Zaprojektowanie uniwersalnego muzeum na pustyni nie jest kwestią redystrybucji prawdopodobieństwa ani zastąpienia jednego przypadku innym w ustalonym wszechświecie przypadków, ani nawet kwestią zmiany punktu widzenia ustalonej przestrzeni zdarzeń. Jest powtórzeniem w sensie metafizycznym; jest architekturą doświadczającą końca swojego świata, a nie tylko badającą granice swego wszechświata. Luwr zostaje pochłonięty przez trzęsienie ziemi nie tyle realne, co konceptualne. Ziemia, która w tym przypadku się trzęsie, nie jest tą, która każe architektowi zbudować replikę oryginalnego modelu czy jego współczesną reinterpretację, lecz leży ona głębiej.
Miasta, a nie tylko pojedyncze budynki, są niszczone przez trzęsienia ziemi, dlatego powinny zajmować naczelne miejsce w estetyce kontyngencji, gdzie byt przeplata się z niebytem, a fulguracja z anihilacją. Miasta, z ich sieciami obiegu i komunikacji, z ich całym językiem, są ważniejsze od pojedynczego budynku, gdy osuwa się cały grunt, i z tego powodu Jean Nouvel mierzy się ze swoim konceptualnym/kontekstualnym trzęsieniem ziemi, budując muzeum, które wyrasta na pustyni jako całe miasto. Kataklizm staje się częścią architektury i nie jest już fazą wstępną. Moment zrównania miasta z ziemią nie następuje już przed momentem jego odbudowy; stają się one jednym i tym samym momentem. W tym tkwi wyjątkowość pustynnego Luwru i jest logiczne, że powinien być on oznaczony fenomenalnym znakiem – w tym przypadku ogromną kopułą przykrywającą całe miasto.
Architekt nie znalazł materiałów do odbudowy Paryża po konceptualnym trzęsieniu ziemi w jego podglebiu, ale w głębszej warstwie – a nawet głębszej koncepcji – ziemi. Ziemia nie dostarczyła tym razem fragmentów Paryża, ale przyniosła ze sobą cały Paryż czy też jego anamorfozę. Architektura znalazła nową zmienną tkwiącą u podstaw jej funkcji, nie kreując już miejsca na ziemi, lecz budując poprzez ziemię. Wszelka architektura została przemieszczona. Metaliczna kopuła pustynnego Luwru waży dokładnie tyle samo, co wieża Eiffla. Moglibyśmy powiedzieć, że jest dokładnie tym, co wieża Eiffla, tyle że przekształconym przez ziemię: nowa uniwersalna wystawa paryska nad nowym uniwersalnym muzeum.
Architekt zalewa miasto światłem płynącym przez ażurową kopułę. Przekształca to, co najpowszechniejsze i najbardziej przytłaczające na pustyni, czyli światło, w to, co najrzadsze i najcenniejsze, czyli deszcz, tworząc „ulewę światła”. Nie jest jasne, czy ów gigantyczny durszlak wynurzył się z piasku, z morza, czy spadł z nieba. Jest rzeczą logiczną, że żywioły się ze sobą mieszają, gdy architektura przekracza własne granice, a pochodzenie światła i geometrii poddawane jest próbie. Zagęszczenie w jedyności jest takie, że kopuła równie dobrze może być złożonym kryształem zrodzonym przez otchłanną pracę ziemi.
7. Ziemia
Hala Wardé, z którą Nouvel współpracował przy pustynnym Luwrze, urodziła się w Bejrucie. Jej rodzina pochodzi z Damaszku. Jeżeli Nouvel może przypisywać sobie autorstwo koncepcji i formy, to Wardé odpowiada za ziemię, która zrodziła materialny konstrukt. Każdy zaprojektowany detal, każda zmontowana konstrukcja i każdy przeprowadzony proces był efektem pracy libańsko-francuskiej architektki i jej zespołu. Biorąc pod uwagę epokowe znaczenie wydarzenia, jakim jest pustynny Luwr, można spróbować wyobrazić sobie jego zdumiewającą realizację, co jest zadaniem niemożliwym, albo uznać, że cały materialny scenariusz spoczywa w archiwach firmy Wardé. W tym sensie, w jakim położyła kres uniwersalnemu programowi Hilberta, procedura arytmetyzacji Gödla nie czyniła nic innego.
Fascynujące jest patrzeć, jak Nouvel odpowiedział na uniwersalność problemu, który przed nim postawiono (podwójną uniwersalność, jako się rzekło); jak stworzył miasto, geometrię, niebo i prawie światło, niemal z niczego, z pustyni, z samego krańca swego wszechświata i jego kodów. Ciekawie będzie następnie porównać, co Wardé, która była ziemią tam, gdzie Nouvel był trzęsieniem ziemi i fulguracją, zrobi po tym wszystkim i jaki budynek teraz zaprojektuje.
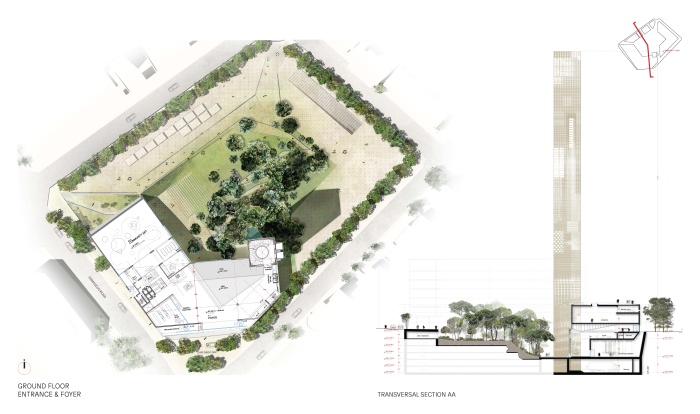
Muzeum Sztuki w Bejrucie: plan i przekrój. (c) HW Architecture
Otchłań zostaje pchnięta w przeciwnym kierunku, a miastem jest oczywiście Bejrut. Miasto światła mogło narodzić się ponownie na pustyni w nowej formie, lecz problem Wardé, która wygrała konkurs na projekt Muzeum Sztuki w Bejrucie (BeMA), jest poważniejszej natury. Jak sprawić, żeby ponownie narodził się Bejrut, miasto końca prawdopodobieństwa i siedmiu trzęsień ziemi? Jak budować nie nad otchłanią, ale poprzez otchłań? Co miałoby być następne, jeśli nie wywrócenie świata na nice?
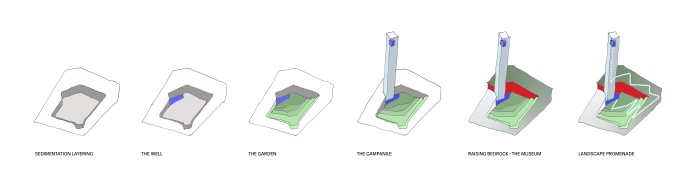
Muzeum Sztuki w Bejrucie. Kolejność prac. (c) HW Architecture
Działka, na której ma powstać BeMA, znajduje się na samym początku Drogi Damasceńskiej, obok budynku Corma i muzeum kryształów i minerałów. Rdzeń nazwy Bejrut, słowo „bîr”, oznacza studnię. I to właśnie studnię wywierciła Wardé, kopiąc fundamenty swego budynku. Woda, płynąc ku powierzchni ziemi, nie mogła nie stworzyć ogrodu, a ziemia, złożona w jednym miejscu, stworzyła wzniesienie, pod którym mieści się samo muzeum.
Otchłań jednak nie byłaby spełniona, gdyby świat nie mógł stworzyć dla niej przeciwwagi. Wardé osiągnęła to za pomocą kampanili, smukłej wieżycy o praktycznie nieskończonej wysokości i nieskończonym ładunku. W teorii prawdopodobieństwa nazywa się to dystrybucją Diraca. W rzeczywistości mamy tu do czynienia z mocnym znakiem, znanym jako alef.
Tłumaczenie z języka angielskiego Marcin Wawrzyńczak
BIO
Elie Ayache urodził się w 1966 w Libanie. Studiował inżynierię na paryskiej École Polytechnique, a następnie pracował jako makler opcji na giełdach MATIF (1987–1990) i LIFFE (1990–1995). Zainteresowanie filozofią prawdopodobieństwa skłoniło go do podjęcia studiów podyplomowych na Sorbonie. Następnie zwrócił się ku technologii wyceny instrumentów pochodnych, co zaowocowało w 1999 r. założeniem firmy ITO 33, produkującej oprogramowanie finansowe. Dzisiaj ITO 33 wiedzie w dziedzinie wyceny obligacji zamiennych, zadłużenia firm i ogólnie kalibracji oraz rekalibracji powierzchni zmienności. Ayache opublikował wiele artykułów na temat filozofii kontyngentnych roszczeń. Autor książek The Blank Swan: The End of Probability (2010) oraz The Medium of Contingency: An Inverse View of the Market (2015).
*Zdjęcie okładki: Warianty fasady budynku Muzeum Sztuki w Bejrucie, (c) HW Architecture
[1] Ian Hacking, The Taming of Chance, Cambridge University Press, Cambridge 1990.
[2] Tegoż, The Emergence of Probability, Cambridge University Press, Cambridge 1975.
[3] Lawrence Sklar, Physics and Chance, Cambridge University Press, Cambridge 1993.
[4] Markus Gabriel, Why the World Doesn’t Exist, Polity Press, Cambridge, Walden 2015.
[5] Elie Ayache, The Blank Swan: The End of Probability, John Wiley & Sons, Chichester 2010; tegoż, The Medium of Contingency: An Inverse View of the Market, Palgrave Macmillan, Basingstoke, Nowy Jork 2015.